Definida por Euclides em 300 a.C., a razão áurea é obtida pela divisão de reta AB por um ponto C, de tal forma que se obtenha uma proporção de AC / AB = CB / AC. O valor dessa razão é um número irracional “que nunca termina e nunca se repete”, representado pela letra grega Fi e vale 1,61803398874989...
Mario Livio, astrofísico romeno, percorre de forma rigorosa os fundamentos da razão áurea e sua aplicação ou citação ao longo dos períodos históricos. O livro ganhou dois prêmios importantes, o Peano Prize (2003) e o “International Pythagoras Prize” (2004). A resenha que se segue, no entanto, destaca a relação da Razão Áurea com a arquitetura e universo artístico, ou seja, prioriza a presença da matemática na estética em detrimento da presença da estética na matemática, discussão mais próxima à linha de investigação proposta no livro.
Inicialmente, o autor descreve o surgimento dos números e o amadurecimento da geometria e das aplicações do número Fi para, em seguida, explicitar sua importância matemática e, também, desmistificar as polêmicas de sua aplicação no campo artístico: nas tabuletas cuneiformes da Babilônia, nas Pirâmides, no Partenon, na obra de Seurat, de Mondrian, dentre outros.
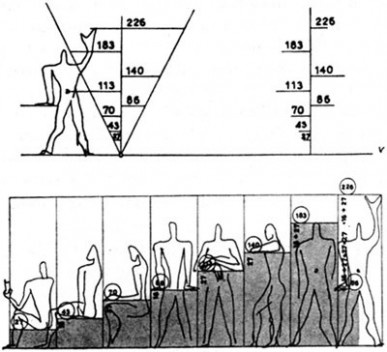
A principal estratégia do autor para situar historicamente a questão é defender que, apesar dos avanços do conhecimento sobre a Razão Áurea, o grande salto (e conseqüente popularidade do tema) só ocorreu no renascimento através dos trabalhos de Leonardo Fibonacci (1170-1240). Entre muitas associações Fibonacci foi o primeiro a associar a Razão Áurea, a Espiral Logarítmica e as ocorrências naturais que influenciaram as pesquisas de Piero della Francesca, Leonardo da Vinci, Albrecht Durer e Luca Pacioli, este último o primeiro a nomear a Razão Áurea como sendo a Proporção Divina. No entanto, o autor argumenta e apresenta opiniões que defendem que nas obras renascentistas, a presença de proporções simples, como a vitruviana, é mais provável que a adoção pela Razão Áurea. Da mesma forma, séculos depois, no cubismo, o autor explica que a aproximação com o conceito está mais relacionada à opção dos artistas em “ressaltar seu interesse geral por questões que relacionam a arte com a ciência e a filosofia” (194) do que à aplicação direta do número Fi. Um dos poucos artistas citados no livro que adotou de fato a Razão Áurea em discurso e projeto foi o arquiteto Le Corbusier e seu modelo de padronização Modulor, que “daria proporções harmoniosas a tudo” (198), capazes de relacionar a mecânica com a escala humana.
Na conclusão do trabalho o autor apresenta questões sobre a presença da estética na matemática e os fundamentos da disciplina. A primeira questão em relação ao fato de uma matemática pura se tornar aplicada, ou seja, por que, por exemplo, uma curva explorada por geômetras gregos pode explicar as órbitas dos planetas ao redor do sol? Relacionado a esse tema, seria a matemática universal e eterna (visão platônica) ou a matemática só existe no cérebro humano (visão intuicionista)? A matemática oferece a explicação dos fenômenos físicos ou estes poderiam ser explicados de diferentes formas? Se a segunda opção for verdadeira, o que define a validade das teorias e como ocorrem os grandes saltos de conhecimento? Acredito que o autor aprofundará essas questões em seu mais recente livro “Is God A Mathematician?” (2009).
Para a arquitetura, a principal contribuição do trabalho é a importância que ele dá à identificação dos “critérios que nos permitirão determinar se certas afirmações sobre o aparecimento da Razão Áurea são verdadeiras ou falsas” (61) e o alerta de que “o jogo de se tentar encontrar a Razão Áurea nas dimensões dos objetos é enganoso” (61). O alerta é fundamental para um contexto que combina dois aspectos: (a) a extrema facilidade de acesso à informação inconsistente e superficial on line, que reforça a falta de rigor relacionado ao tema; e (b) a busca cada vez mais freqüente na arquitetura por atalhos, muletas e aproximações fáceis, por exemplo, com o universo orgânico ou científico.
De todo modo, as questões expostas pelo autor trafegam com a mesma indefinição no campo da arquitetura e, de forma mais específica, na presença da matemática pura ou aplicada na disciplina. Por que a arquitetura recorreria à Razão Áurea? As grandes obras são aquelas que, consciente ou inconscientemente, a utilizaram? Existe uma harmonia arquitetônica universal e eterna? Existe probabilidade de a harmonia na arquitetura ser a mesma do mundo natural? Na arquitetura, a Razão Áurea deve ser adotada em relação às obras orgânicas, nas estruturas inspiradas na natureza ou nos sólidos geométricos complexos? Com a incorporação de novas tecnologias de projeto e execução – presente na atual proliferação da arquitetura high tech, por exemplo – a incorporação da Razão Áurea parece ser facilitada pela inserção de um dado a mais na equação ou no programa computacional que auxilia o projeto do edifício. Faria sentido?
Sobre essa busca de cânone para a beleza ideal na aplicação da Razão Áurea, o autor é contundente e nos sugere a “desistir de suas aplicações como padrão fixo de estética, seja na forma humana, seja como uma pedra fundamental das belas artes” (226).
sobre o autor
Daniel Medeiros de Freitas é arquiteto (2000), especialista em revitalização urbana e arquitetônica (2004) e mestre em urbanismo (2006). É professor assistente do curso de arquitetura e urbanismo da UNA-Bhte