Gallerie des Machines, Paris, 1889
[fonte: Cortesia Bildarchiv Foto Marburg]

Beatriz de Abreu e Lima: O senhor trabalha com diagramas conceituais, como aqueles usados na Arquitetura?

Charles Walker: Sim, mas os engenheiros sempre trabalharam com diagramas. Quando uma estrutura é analisada, ela sempre é reduzida a um diagrama simples, normalmente conhecido, como por exemplo, uma viga com condições de apoio determinadas. Temos fórmulas analíticas para representar vigas apoiadas de diversas maneiras. Os engenheiros sempre reduzem as coisas a partes diagramáticas simples. Este tipo de abstração sempre foi usado na Engenharia. Acho que hoje em dia estamos indo além, porque estamos nos movendo em direção aos diagramas não-lineares, diagramas com um alto grau de redundância (10) e um alto grau de complexidade.

BAL: Redundância?

CW: Bem, quando algo é estaticamente determinado não há redundância [constitui, portanto, um sistema isostático], o que significa que pode ser resolvido; pode ser resolvido analiticamente de uma maneira muito simples, como um arco triarticulado. Por exemplo, na Galerie des Machines em Paris [Projeto do arquiteto Ferdinand Dutert, para a Exposição Mundial de Paris de 1889], um arco tri-articulado com três grandes pinos foi realmente construído e os pinos foram produzidos utilizando-se moldes do tamanho de um automóvel. Ao passo que hoje, os engenheiros podem analisar um arco sem pinos, hiperestático ao terceiro grau, ou seja, os três pinos podem “abrir” [sem comprometer a estrutura], porém, já estamos analisando estruturas que são hiperestáticas ao décimo milésimo grau. São análises que nunca poderiam ser realizadas manualmente com um simples diagrama conceitual, porque existem coisas como estruturas não-lineares que são de uma ordem de complexidade mais difícil de ser analisada.

BAL: É interessante ouvir este termo: estruturas não-lineares...

CW: Acho que existe uma grande diferença, que nem sempre é entendida, entre as soluções analíticas e as soluções numéricas. Uma solução analítica resulta de uma busca por uma regra geral. Estudamos um problema e encontramos uma solução geral para o problema. Ao passo que uma solução numérica resulta da produção do modelo numérico de uma estrutura, que resolve aquela estrutura em particular. O que eu quero dizer, é que hoje em dia, estamos buscando cada vez mais soluções numéricas, digitais, para uma estrutura específica, para um problema específico. Não estamos mais buscando regras gerais ou universais como acontecia nos anos 50, quando as pessoas estavam desenvolvendo as teorias das cascas, trabalhando analiticamente, buscando princípios de comportamento. Acho que hoje não estamos tão interessados nisso. De certa forma, esse tipo de projeto analítico está bastante ultrapassado e estamos começando a nos direcionar para a resolução de problemas específicos, como as estruturas que possuem uma certa complexidade ou redundância inerente e que não conduzem a uma regra geral.

nota

10
Redundâncias em estruturas são os elementos ou apoios estruturais que excedem aqueles necessários em uma estrutura estaticamente determinada, ou seja, em uma estrutura isostática. Estrutura isostática: estrutura cujas solicitações podem ser calculadas com o auxílio exclusivo das leis da estática; o número de vínculos é o estritamente necessário para impedir movimento. Estrutura hiperestática: estruturas submetidas à esforços cujo cálculo não pode ser efetuado por meio das leis da estática; o número de vínculos é maior que o número necessário e a estrutura não apresenta movimento mesmo retirando-se algum vínculo. Grau de hiperestaticidade é o número máximo de vínculos que podem ser suprimidos em uma estrutura sem que esta se torne hipostática. Estrutura Hipostática: estrutura que pode apresentar movimento; o número de vínculos é menor que o necessário.

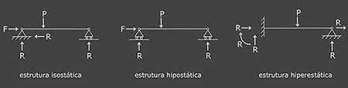
Situações de equilíbrio das estruturas